TUGAS 4 "ALJABAR BOOLEAN"

4A. PEMBUKTIAN PERSAMAAN ALJABAR BOLEAN.

T1. Hukum Komutatif

       (a). A+B = B+A

       (b). A.B  = B.A

T2. Hukum Asosiatif

a.      (A+B)+C = A+(B+C)

b.      (AB) C = A (BC)

 T3. Hukum Distributif

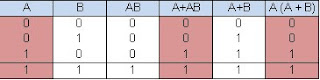
a.      A(B+C) = AB + AC

b.      A +(BC) = (A+B) (A+C)

T4. Hukum Identity

(a)   A + A = A

(b)    A A = A

 

T5. (a) AB+AB'=A

       (b) (A+B)(A+B')= A

 

T6. Hukum Redudansi

(a) A + A B = A
(b) A (A + B) = A

 

T7

(a) 0 + A = A
(b) 0 A = 0

 

T8

(a)   1 + A = 1

(b)   (b) 1 A = A

 

T9

(a) A' +A=1
(b) A' A = 0

T10

(a) A+A' B= A+B
(b) A(A' + B) = AB

T11. TheoremaDe Morgan's

            (a) (A+B)' A' B'
            (b) (AB)' = A' + B' 

 

4B. Quiz Aljabar Boolean

---

1. Give the relationship that represents the dual of the Boolean property A + 1 = 1?
   (Note: * = AND, + = OR and ' = NOT)
1. A * 1 = 1
2. A * 0 = 0
3. A + 0 = 0
4. A * A = A
5. A * 1 = 1

SEBAB :

A	1	A+1	A*0	0
0	1	1	0	0
1	1	1	0	0

2. Give the best definition of a literal?
1. A Boolean variable
2. The complement of a Boolean variable
3. 1 or 2
4. A Boolean variable interpreted literally
5. The actual understanding of a Boolean variable

SEBAB : A literal = 1 atau 2

3. Simplify the Boolean expression (A+B+C)(D+E)' + (A+B+C)(D+E) and choose the best answer.
1. A + B + C
2. D + E
3. A'B'C'
4. D'E'
5. None of the above

Sebab : (A+B+C)(D+E)+(A+B+C)(D+E) = A+B+C

4. Which of the following relationships represents the dual of the Boolean property x + x'y = x + y?
1. x'(x + y') = x'y'
2. x(x'y) = xy
3. x*x' + y = xy
4. x'(xy') = x'y'
5. x(x' + y) = xy

Sebab : x+x’y =x+y ekuivalen dengan x(x’+y)=xy

5. Given the function F(X,Y,Z) = XZ + Z(X'+ XY), the equivalent most simplified Boolean representation for F is:
1. Z + YZ
2. Z + XYZ
3. XZ
4. X + YZ
5. None of the above

Sebab : fungsi yang tepat adal F(X,Y,Z)=Z

6. Which of the following Boolean functions is algebraically complete?
1. F = xy
2. F = x + y
3. F = x'
4. F = xy + yz
5. F = x + y'

Sebab : F(x,y)= x+y’ bisa menggunakan fungsi AND, OR, NOT . F ini adalah aljabar sempurna. Contoh : NOT: F(0,B)=B’ || OR : F(A, F(0,B))=A+B ||  AND:F(0,F(F(0,A),B))=A*B

7. Simplification of the Boolean expression (A + B)'(C + D + E)' + (A + B)' yields which of the following results?
1. A + B
2. A'B'
3. C + D + E
4. C'D'E'
5. A'B'C'D'E'

Dengan contoh x + xy = x, dengan x=(A+B)’=A’ B’ dan y=(C+D+E)’ = C‘D’E’

8. Given that F = A'B'+ C'+ D'+ E', which of the following represent the only correct expression for F'?
1. F'= A+B+C+D+E
2. F'= ABCDE
3. F'= AB(C+D+E)
4. F'= AB+C'+D'+E'
5. F'= (A+B)CDE

Sebab : persamaan diatas menggunakan persamaan DEMORGAN

9. An equivalent representation for the Boolean expression A' + 1 is
1. A
2. A'
3. 1
4. 0

Alasan : Dari contoh boolean A+1 = 1, A=A.

10. Simplification of the Boolean expression AB + ABC + ABCD + ABCDE + ABCDEF yields which of the following results?
1. ABCDEF
2. AB
3. AB + CD + EF
4. A + B + C + D + E + F
5. A + B(C+D(E+F))

Alasan mengulang dari teori ASOSIATIF    x+xy= x.